[그래프/정렬/유향] 위상정렬 / Topological Sorting

위상정렬 / Topological Sorting

 유향 비순환 그래프(Directed Acyclic Graph, DAG) 에서 각 노드들을 선형 순서로 나열하는 방법입니다. 여기서 유향 비순환 그래프란, 방향이 있는 그래프 중에 사이클이 없는 그래프를 말합니다. 위상 정렬은 보통 의존 관계를 해결할 때 사용되며, 그래프 내에서 어떤 일의 순서를 정하거나 작업 간의 선후 관계를 정의하는 문제를 풀 때 유용합니다.

위상 정렬의 조건

그래프는 반드시 유향 비순환 그래프(DAG)이어야 합니다.

• 유향(Directed): 간선의 방향이 있다.
• 비순환(Acyclic): 사이클이 존재하지 않는다. 즉, 위상 정렬은 순환하는 경로가 있으면 불가능합니다.

위상 정렬의 동작 원리

위상 정렬의 핵심은 선행 조건을 만족하는 노드부터 순차적으로 처리하는 것입니다. 즉, 어떤 노드를 처리하려면 그 노드에 들어오는 모든 간선을 먼저 제거해야 합니다. 이를 통해 의존성이 있는 작업들이 먼저 처리되며, 나중에 의존하는 작업들을 차례로 수행할 수 있습니다.

위상 정렬의 활용

위상 정렬은 다음과 같은 다양한 문제들에 유용하게 사용됩니다.

1. 작업 스케줄링: 작업 간의 의존 관계가 있는 경우, 어떤 작업을 먼저 수행해야 할지 결정할 때 사용됩니다.
2. 컴파일러: 프로그램의 컴파일 순서를 정할 때, 각 모듈 간의 의존 관계를 위상 정렬로 해결할 수 있습니다.
3. 과목 수강 순서: 선수 과목이 있는 학과에서 수강 순서를 결정할 때 활용됩니다.
4. 프로젝트 관리: 프로젝트 내 여러 태스크의 의존성을 해결하는 데 사용될 수 있습니다.

위상 정렬의 대표적인 알고리즘

1. Kahn's Algorithm (차수 기반 접근)
2. DFS(Depth First Search)를 활용한 방법

 

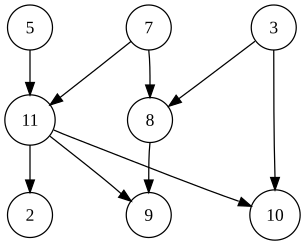왼쪽의 그래프는 많은 유용한 위상 정렬을 보여준다. 5, 7, 3, 11, 8, 2, 9, 10 ( 맨 위에서 왼쪽에서 오른쪽으로 아래까지 ) 3, 5, 7, 8, 11, 2, 9, 10 ( 제일 작은 수부터 이용 가능한 첫 꼭짓점까지 ) 5, 7, 3, 8, 11, 10, 9, 2 ( 왼쪽 맨 위를 처음으로 ) 7, 5, 11, 3, 10, 8, 9, 2 ( 가장 큰 수부터 이용 가능한 첫 꼭짓점까지 ) 7, 5, 11, 2, 3, 8, 9, 10 ( 맨 위부터 왼쪽에서 오른쪽으로 시도하여 아래까지 )3, 7, 8, 5, 11, 10, 2, 9 ( 제멋대로 )

 

2252번. 줄 세우기

Kahn's Algorithm을 사용한 Swift code

import Foundation

struct Queue<T> {
    var index: Int = 0
    var queue: [T] = []

    public var isEmpty: Bool {
        return queue.count == index
    }

    mutating func push(_ e: T) {
        queue.append(e)
    }

    mutating func pop() -> T? {
        if !self.isEmpty {
            let element = queue[index]
            index += 1
            return element
        }
        return nil
    }
}

func topologicalSort(n: Int, m: Int, edges: [(Int, Int)]) {
    var graph = Array(repeating: [Int](), count: n + 1)
    var inDegree = Array(repeating: 0, count: n + 1)
    
    for (x, y) in edges {
        graph[x].append(y)
        inDegree[y] += 1
    }
    
    var q = Queue<Int>()
    for i in 1...n {
        if inDegree[i] == 0 {
            q.push(i)
        }
    }
    
    var result: [Int] = []
    
    while !q.isEmpty {
        if let current = q.pop() {
            result.append(current)
            
            for next in graph[current] {
                inDegree[next] -= 1
                if inDegree[next] == 0 {
                    q.push(next)
                }
            }
        }
    }
    
    for student in result {
        print(student, terminator: " ")
    }
    print()
}

let nm = readLine()!.split(separator: " ").map{Int(String($0))!}
let (n, m) = (nm[0], nm[1])
var edges: [(Int, Int)] = []

for _ in 0..<m {
    let edge = readLine()!.split(separator: " ").map{Int(String($0))!}
    edges.append((edge[0], edge[1]))
}

topologicalSort(n: n, m: m, edges: edges)

1516번. 게임 개발

DP와 위상정렬을 사용한 c++ code

#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int main() {
  int n;
  cin >> n;

  vector<vector<int>> graph(n + 1);
  vector<int> in_degree(n + 1, 0);
  vector<int> build_time(n + 1, 0);
  vector<int> total_time(n + 1, 0);

  for (int i = 1; i <= n; i++) {
    cin >> build_time[i];
    int input;
    while (true) {
      cin >> input;
      if (input == -1) break;
      graph[input].push_back(i);
      in_degree[i]++;
    }
  }

  queue<int> q;

  for (int i = 1; i <= n; i++) {
    if (in_degree[i] == 0) {
      q.push(i);
      total_time[i] = build_time[i];
    }
  }

  while (!q.empty()) {
    int current = q.front();
    q.pop();

    for (int next : graph[current]) {
      in_degree[next]--;

      total_time[next] =
          max(total_time[next], total_time[current] + build_time[next]);

      if (in_degree[next] == 0) {
        q.push(next);
      }
    }
  }

  for (int i = 1; i <= n; i++) {
    cout << total_time[i] << "\n";
  }

  return 0;
}

 

출처

위상정렬 - 위키백과, 우리 모두의 백과사전